2. Digits

Find the number of digits in a nonnegative integer n.

Input. One nonnegative integer n (0 ≤ n ≤ 2*10⁹).

Output. The number of digits in number n.

Sample input	Sample output
13243	5

SOLUTION

elementary problem

Algorithm analysis

The number of digits in a number can be found:

· using one loop.

· in recursive way, using the recurrence relation:

digits(n) =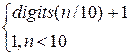

Algorithm realization

Read the input value n. If n = 0, the answer is 1. Otherwise initialize res with 0 and compute the number of digits in n using a while loop.

scanf("%d",&n);

res = (n == 0);

while(n > 0)

{

n /= 10;

res++;

}

printf("%d\n",res);

Algorithm realization – recursive

#include <stdio.h>

int n, res;

int digits(int n)

{

if (n < 10) return 1;

return 1 + digits(n / 10);

}

int main(void)

{

scanf("%d",&n);

res = digits(n);

printf("%d\n",res);

return 0;

}

Java realization

import java.util.*;

public class Main

{

static int digits(int n)

{

if (n < 10) return 1;

return 1 + digits(n / 10);

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

int res = digits(n);

System.out.println(res);

con.close();

}

}

Python realization

Convert the input number n to a string, and then find its length.

n = int(input())

print(len(str(n)))

If there are spaces before the number, then the following implementation will fail:

s = str(input())

print(len(s))

Implementation with while loop:

x = int(input())

cnt = 0

if x == 0:

print ("1")

else:

while x > 0:

cnt += 1

x = x // 10

print (cnt)

Python realization – recursion

def f(n):

if n < 10:

return 1

return f(n / 10) + 1

n = int(input())

print (f(n))